Robotics - [2D SLAM 2] Map Generation

Submap Generation

In modern robotics mapping systems, efficient environment representation and robust localization are achieved by dividing the map into smaller, manageable submaps. Each submap is built upon two key components: an occupancy map that records obstacles and free space, and a likelihood field derived from the occupancy map. The workflow of submap generation is as follows:

1. Initialize the occupancy map with the first scan.
2. Generate a likelihood field according to the scan
3. For subsequent scans:
   1. Perform Scan-match against the likelihood to find the pose estimate from the last scan T_21.
   2. If T_21 shows a translation or a rotation larger than their thresholds. The current scan is a keyframe.
   3. Add the keyframe into the occupancy map.
   4. Generate a likelihood field according to the scan
   5. Create a new submap with its origin being the current scan’s origin, if any below condition is met:
      1. The occupancy map already has N submaps
      2. Any point already falls outside of the map boundary.

In practice, bresenham line algorithm is a good alternative for generating occupancy map. Each cell in an occupancy map is technically a 2D Logit:

\[\begin{gather*} \begin{aligned} & p = log(\frac{x}{1-x}) \end{aligned} \end{gather*}\]

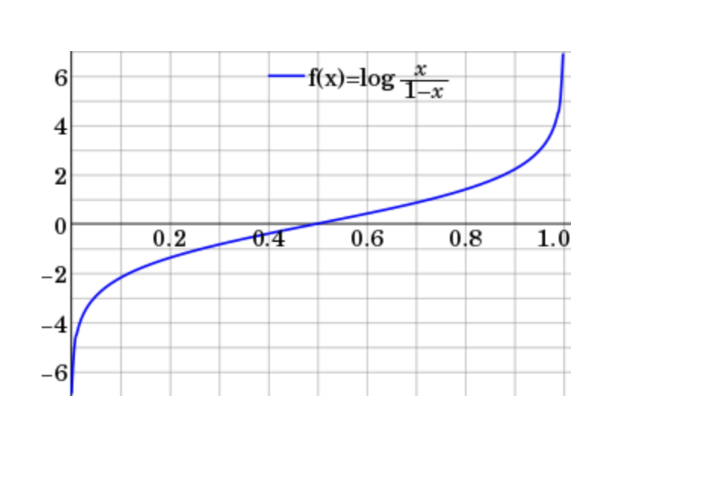
In practice a simplified binary assignment (using +1 and -1) produces similar results. This approach reduces computational complexity and implementation overhead while still capturing the essential behavior of the system.

Loop Closure

Multi-resolution Scan Matching

1. Generate M likelihood fields of different sizes and resolutions. Also, generate one template (neighborhood of any scan point)
   • For the first scan, we simply add it to the occupancy map, then initialize likelihood fields with it.
2. Iterate through the likelihood field pyramid, from the lowest resolution to the highest:
   1. Build a graph of the pose estimate (vertex) and distance errors of scan points (edges)
   2. Set $\delta$ in $\Chi^2$ of an edge. Above $\delta^2$, a g2o edge is considered an outlier in the data. Then these large errors will be downweighted: \(\begin{gather*} \begin{aligned} & \frac{1}{2} (y_i - \hat{y}_i)^2, \text{for} |y_i - \hat{y}_i| < \delta \\ & \delta |y_i - \hat{y}_i| - \frac{1}{2} \delta^2, \text{otherwise} \end{aligned} \end{gather*}\)

      1
      2
      3
       auto rk = new g2o::RobustKernelHuber;
       rk->setDelta(delta);
       edge->setRobustKernel(rk);
      

   3. Count number of inliers, that is, edges with $Chi^2$ lower than its threshold. If there are not enough inlier, we are not going to add the scan for loop closure / registration
   4. Keep the pose estimate for next level likelihood field optimization
3. Update occupancy grid

Important parameters:

• Matched Scan point (inlier) ratio:
  • If this ratio is too high, a loop is considered not detected and we will lose potential constraints there.
  • If used in scan registration, one might notice that earlier scans are not added. This will decline further scan additions.
• Thresholds of free / occupied cell values for Visualization:
  • This can create a huge impact of the resulted map (TODO: comparison)

Loop Closure

Say submap1 has world pose: T_w_m1, submap 2: T_w_m2. a particular scan is T_w_s. The transform between the two submaps are: T_m1_m2. In a pose graph, this is one “adjacent edge”.

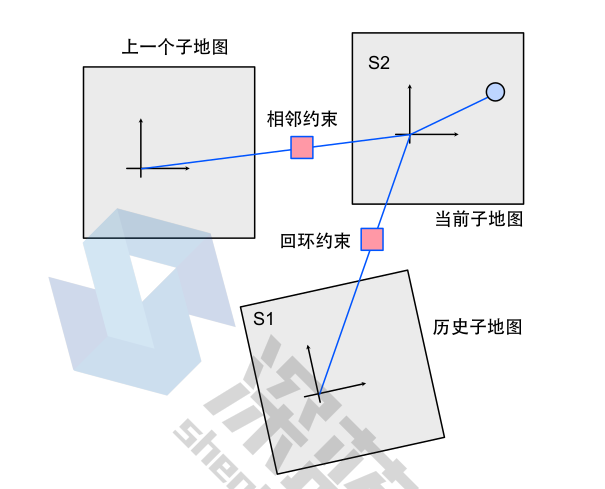
We also want to construct a loop closure edge. That is done by:

\[\begin{gather*} \begin{aligned} & T_{m1, m2} = T_{w, s1} T_{s1, s2} T_{s2, w} \\ & e = log(T_{m1, m2}) \end{aligned} \end{gather*}\]

The Jacobian of the above is dependent on x, y, theta of both submap poses. It’s quite complex and we can leave that to g2o’s auto differentiation.

Loop Closure Detection And Optimization

• Policies for loop candidate detection:
  • We check for matching between the current frame and past submaps. (Which can be improved for larger maps for sure)
    • Skip the submap if it’s too recent to the last submap
    • Skip the submap if it already has a valid loop-closing constraint with the current submap
    • Check if the frame pose and submap pose is within a cartesian distance threshold
    • Add the submap id to a vector as a candidate
• Match in history submaps:
  • For each loop candidate detection:
  • Get the mr field of the submap
  • Perform scan matching using the mr field with a point matching threshold.
  • If there’s a loop closure, we add a loop-closing constraint between the past submap and the current submap to a vector
• Optimization:
  • add all submap poses as vertices
  • add the edges between consecutive maps to g2o as consecutive edges. The measurement is simply T_12
  • add valid loop-closing constraints to g2o as loop-closing edges
  • Run optimizer
• For all loop closing edges,
  • if the edge is valid, set robust kernel to nullptr so it will contribute fully without being downweighted by the kernel
  • if the edge is invalid, set level to 1. Typically, only level=0 edges are used for optimization
  • Run optimizer again
• Get updated poses and update them in the associated submap

Final Submap Genenration

This is what the pipeline looks like:

• Assumptions:
  • Submaps have unique ids
• Set up
  • each submap has an additional multi-resolution likelihood field for loop closure detection.

1. Add a new submap
2. Upon Receiving a new frame:
   • Check if it’s a keyframe by distance threshold
3. If the new frame is a keyframe:
   1. Add the keyframe to the current submap
      • Add the keyframe to both the occupancy grid and the likelihood field
   2. Trigger loop detection and optimization (See the above Loop Closure Detection And Optimization section)
4. If the keyframe pose has moved out of the current submap bounds, or there are too many keyframes, create a new submap:
   • Copy N key frames from the previous frame

---

• Previous
  Robotics - [2D SLAM 1] Introduction and Scan Matching
• Next
  Robotics - Gauss Newton (GN) and Levenberg Marquardt (LM) Optimizers

---