Activation Functions
Early papers found out that Rectified Linear Unit (ReLu) is always faster than Sigmoid because of its larger derivatives, and non-zero derivatives at positive regions.
However, now with more tricks like batch normalization,
- ReLu:
y=max(0, x), atx=0it’s technically non-differentiable. But we can still fake it simply:y' = 0 or 1ReLu - Advantages:
- This helps avoid diminishing derivatives? because large values have derivative being 1.
- Computational efficiency. Easy to compute.
- It outputs zero on negative values, which makes forward pass compute less, as well as the backward pass
- Because fewer neurons have non-zero outputs, the less “sensitive” the system is to smaller changes in inputs. Making it a form of regulation. (See the regularization section).
- Disadvantages:
- Exploding gradients: gradient can become large (because TODO?)
- Dead neurons: neurons may not be activated if their weights make the output negative values.
- Unbounded outputs
- Rule Of Thumbs of Applications:
- ReLu should NOT be applied immediately before softmax, because it could distort the relative differences between logits by setting the negative ones to 0.
- Advantages:
- Leaky ReLU: regular ReLU would lead to dead neurons when $x=0$. That could cause learning to be stuck. Leaky ReLU can unstuck this situation by having a small negative slope and allowing backprop flow correspondingly.
ReLu6ReLu 6 = min(max(x, 0), 6). So if there is an overflow, or underflow, outputs could be naturally large, and would be capped just as they would without overflow/underflow.- Activation values now occupy a smaller and fixed range, so in terms of quantization noise, so the representation is with fewer bits.
-
Typically $\alpha=0.01$
-
GELU (Gaussian Error Linear Units)
- ReLu is less common in Transformer due to its dying negative activations. GELU is
x * Cumulative Density Function (CDF) of Gaussian Distribution at point x. - Advantages:
- It’s differentiable all over $\R$. That helps with smoothening hard gradient transitions (like in ReLU)
- Also, it has no dead neurons
- Disadvantages:
- It’s slower
- ReLu is less common in Transformer due to its dying negative activations. GELU is
- tanh: $\frac{2}{1+e^{-2x}}-1$
- Advantages:
- tanh starts from -1 to 1, so if we want negative values in output, go for tanh
- compared to sigmoid, its derivative in
[-1, 1]has a larger range, which could help with the learning process.
- Disadvantages:
- For large and small values, gradients are zero (vanishing gradient problem)
- Could be moderately expensive to train (with exponentials)
- Sigmoid (or “Logistic Function”)
sigmoid - Advantages:
- Disadvantages:
- For large and small values, gradients are zero (vanishing gradient problem)
- Its max is 0.25. This could be a huge disadvantage given that nowadays with more layers, this gradient diminishes fast
- Could be moderately expensive to train (with exponentials)
- For large and small values, gradients are zero (vanishing gradient problem)
Cost Functions
- Mean Squared Error $\frac{1}{n} \sum(y_i-\hat{y}_i)^2$
- Disadvantages:
- Sensitive to outliers with larger errors due to the squaring (especially compared to MAE)
- If errors are non-gaussian, this is probably not robust either.
- Disadvantages:
- Mean Absolute Error $\frac{1}{n} \sum(y_i-\hat{y}_i)$
- Advantages:
- Less sensitive to outliers
- DisadvantagesL
- Not differentiable at 0, which could be problematic, especially jacobians are near zero
- Advantages:
- Hinge Loss: $\frac{1}{n} \sum max(0, 1-y_i\hat{y}_i)$
- Mostly used in SVM training, not working well with probablistic estimations
-
Huber Loss (a.k.a Huber Kernel) \(\begin{gather*} \begin{aligned} & \frac{1}{2} (y_i - \hat{y}_i)^2, \text{for} |y_i - \hat{y}_i| < \delta \\ & \delta |y_i - \hat{y}_i| - \frac{1}{2} \delta^2, \text{otherwise} \end{aligned} \end{gather*}\)
- Advantages:
- It’s continuous and differentiable
- Combines MAE and MSE.
- It’s commonly used in SLAM because it’s more robust to outliers errors.
- It’s quadratic for small errors, preserving the sensitivity there
- It’s linear for larger errors
- Requires tuning $\delta$
- Advantages:
- Sparse Entropy Loss: designed for image segmentation, where one-hot encoding is used in model output (after softmax) but training data only has labels. The loss per pixel is $l = -log(p_{true})$
For example:
For 3 pixels, training data labels are: [2,1,0]
Output data:
\[\begin{gather*} 0.1 & 0.7 & 0.2 \\ 0.3 & 0.7 & 0.0 \\ 0.5 & 0.4 & 0.1 \\ \end{gather*}\]Then, the loss for each pixel is:
\[\begin{gather*} -log(0.2) & -log(0.3) & -log(0.5) \end{gather*}\]You can add up the losses and get the sum of it
========================================================================
Classification Losses
========================================================================
Cross Entropy Loss (Log Loss)
\[-\frac{1}{n} \sum (y_ilog(\hat{y}_i) + (1-y^i)log(1-\hat{y}_i))\]- Advantages:
- Good for classification problems.
- Suitable for probablistic Interpretation, and penalizes wrong confident predictions heavily
- Disadvantages:
- when $y^i$ is (0,1). And the closer it is to the bounds, the loss would be larger
Negative Log-Likelihood Loss (NLL)
Given a number of true classes (like acceptable output words in a sentence generator), NLL measures how likely we get any true class based on our prediction, a log-probability distribution across all outputs.
- Input Requirements: The model’s output should be log-probabilities when using NLL Loss.
- Target Format: The targets should be provided as class indices, not one-hot vectors.
- For M samples,
NLL is always used with log-softmax activations to ensure numerical stability.
NLL Example
- We are given a single example, with logits
logits=[1.0, 2.0, 0.5, ] - Apply log-softmax $log(\frac{exp(x_i)}{\sum_i exp(x_i)})$ and get
[−1.46303, −0.46303, −1.96303, ] - Given a single true class
I=[1], NLL becomes
========================================================================
Multicalss Classification & Image Segmentation Losses
========================================================================
Multiclass classification and image segmentation tasks both suffer the data imbalance problem. E.g., the background in image segmentation, or negative classes in multi-class classification make up around 80%. Do we want to count the accuracies in those areas? Yes. But do we want to treat them equally as the positive object classes? No. Because the positive object classes are fewer, which makes our model more sensitive them.
IoU and Dice Loss
- IoU Loss
IoU loss is:
1 - IoU - Dice Loss is $1 - \frac{2overlap}{\text{total_area}}$
When training accuracy (overlap) increases, IoU loss is more sensitive to it at the very beginning, but not as sensitive when training accuracy is already high. Comparatively, Dice loss is more sensitive in high training accuracies, largely due to 2*overlap. This can be proven by taking the derivative of the two losses.
My implementation:
1
2
intersect = (pred == labels)
dice_loss = 1 - 2 * (intersect.sum().item())/ (pred.shape + labels.shape)
Along with weighted cross entropy loss, Dice loss (or the sensitivity) function were Introduced by Sudre in 2017 [1].
Focal Loss
Focal loss addresses the class imbalance problem by penalizing the correctly idenfied classes. $\gamma$ is a hyperparameter, $p_t$ is the probability of correct classification.
\[\begin{gather*} FL = (1-p_t)^{\gamma} (-log(p_t)) \end{gather*}\]
The above is for image segmentation, where every pixel has only one true label. For multi-class classification problems, one can use FocalLoss as well, but with some adaptations. This post is very well written
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
import torch
torch.set_printoptions(precision=4, sci_mode=False, linewidth=150)
num_label = 8
logits = torch.tensor([[-5., -5, 0.1, 0.1, 5, 5, 100, 100]])
targets = torch.tensor([[0, 1, 0, 1, 0, 1, 0, 1]])
logits.shape, targets.shape
# will all one be better?
def focal_binary_cross_entropy(logits, targets, gamma=1):
"""
The logic of the below is:
- For False Positive: adjusted_p = 1-p (~0), 1-adjusted_p ~1 -> logp = -log(adjusted_p) (far larger than 0)
-> loss = logp * (1-adjusted_p)**gamma = large number ✅
- For False Negative: adjusted_p = p (~0), 1-adjusted_p ~1 -> logp = -log(adjusted_p) (far larger than 0)
-> loss = logp * (1-adjusted_p)**gamma = large number ✅
- For True Negative: adjusted_p = 1-p (~1), 1-adjusted_p ~0 -> logp = -log(adjusted_p) (~0 )
-> loss = logp * (1-adjusted_p)**gamma = ~0 ✅
- For True Positive: adjusted_p = p (~1), 1-adjusted_p ~0 -> logp = -log(adjusted_p) (~0 )
-> loss = logp * (1-adjusted_p)**gamma = ~0 ✅
- torch.clamp() is in place to avoid overflow or under flow
"""
l = logits.reshape(-1)
t = targets.reshape(-1)
p = torch.sigmoid(l)
p = torch.where(t >= 0.5, p, 1-p)
print(f"adjusted probability: {p}")
print(f"1-adjusted_p: {1-p}")
logp = - torch.log(torch.clamp(p, 1e-4, 1-1e-4))
print(f"logp: {logp}")
loss = logp*((1-p)**gamma) #[class_num]
print(f'If the starting index = 1, indices 2, 3, 5, 7 should have a large loss: {loss}')
loss = num_label*loss.mean()
return loss
focal_binary_cross_entropy(logits, targets)
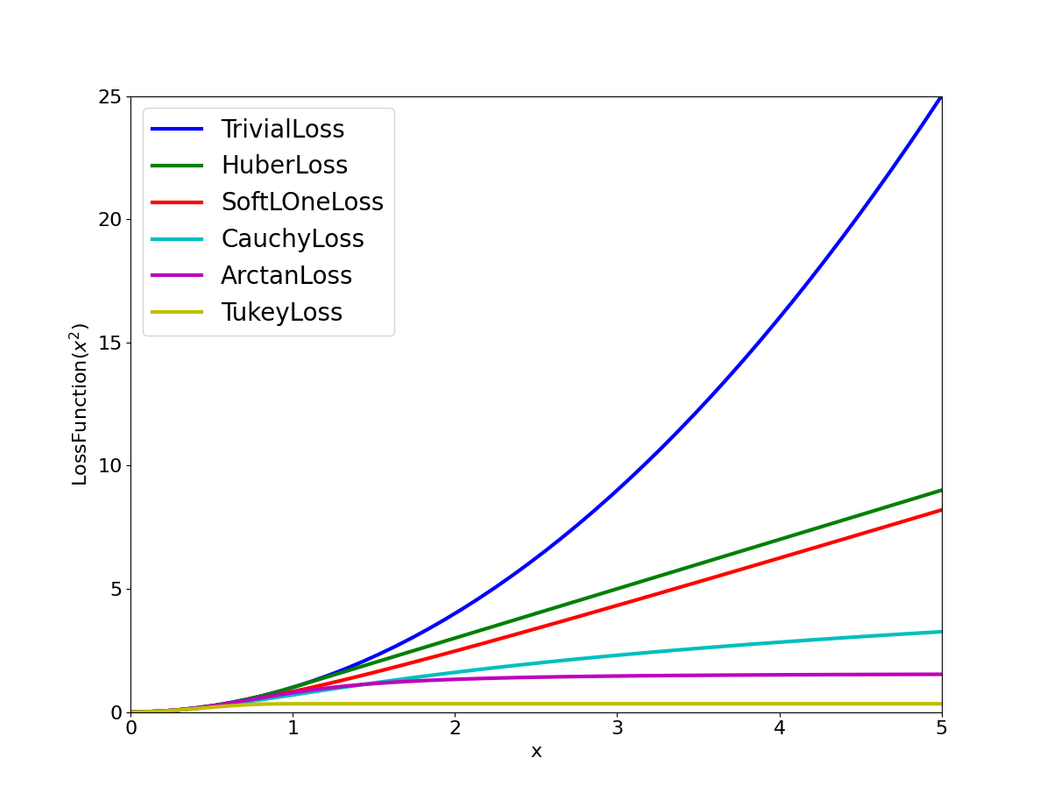
Cauchy Robust Kernel
In typical nonlinear optimization (e.g., SLAM), the squared $L_2$ norm of a residual error $e$ is used as the cost:
\[\begin{gather*} \begin{aligned} & s = e^\top \Omega e \end{aligned} \end{gather*}\]To reduce the influence of outliers, a robust loss function $\rho(s)$ is used in place of the plain quadratic cost. The $\textbf{Cauchy loss}$ is defined as:
\[\begin{gather*} \begin{aligned} & \rho(e) = \delta^2 \ln\left(1 + \frac{e}{\delta^2}\right) \end{aligned} \end{gather*}\]where $\delta$ is a tuning parameter that determines the scale at which residuals begin to be downweighted.
The derivative of the Cauchy loss with respect to $e$ gives the weight applied to the residual during optimization:
\[\begin{gather*} \begin{aligned} & \frac{\partial \rho}{\partial e} = \frac{1}{1 + \frac{e}{\delta^2}} \end{aligned} \end{gather*}\]This expression shows that for large residuals e.g., a wrong observation edge ($s \gg \delta^2$), the weight decreases, thereby reducing their influence in the optimization process.
Unlike the squared $L_2$ loss, which grows quadratically with $s$, the Cauchy loss grows logarithmically:
- For small $s$, $\rho(s) \approx s$ (i.e., behaves like L2).
- For large $s$, $\rho(s)$ grows slowly, and the gradient $\frac{\partial \rho}{\partial s}$ asymptotically approaches zero.
This means the cost function becomes less sensitive to large residuals (outliers), improving robustness in noisy or mismatched data.
References
[1] Sudre, C. H., Li, W., Vercauteren, T., Ourselin, S., & Cardoso, M. J. Generalised Dice overlap as a deep learning loss function for highly unbalanced segmentations. Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support: 3rd International Workshop, DLMIA 2017, and 7th International Workshop, ML-CDS 2017 Held in Conjunction with MICCAI 2017, Quebec City, QC, Canada, September 14, 2017, Proceedings, pp. 240–248. Springer, 2017.