A very nice reference article in Mandarin
Column, Row, Left Null and Right Null Spaces
Given the linear system $A\mathbf{x}=\mathbf{b}$ with $A\in\mathbb{R}^{m\times n}$:
- $\textbf{Row space}$: $\operatorname{Row}(A)$ is the subspace of $\mathbb{R}^{n}$ spanned by the rows of $A$.
- Its dimension equals the rank $r=\operatorname{rank}(A)$.
- $\textbf{Column space}$: $\operatorname{Col}(A)$: the subspace of $\mathbb{R}^{m}$ spanned by the columns of A.
- The system $A\mathbf{x}=\mathbf{b}$ has a (possibly unique) solution iff $\mathbf{b}\in\operatorname{Col}(A)$.
- If $A$ has full column rank ($r=n$), the solution is unique.
- The system $A\mathbf{x}=\mathbf{b}$ has a (possibly unique) solution iff $\mathbf{b}\in\operatorname{Col}(A)$.
- $\textbf{Right nullspace (nullspace)}$: $\mathcal{N}(A)={\mathbf{x}\in\mathbb{R}^{n}\mid A\mathbf{x}=0}$.
- Every vector in $\mathcal{N}(A)$ is orthogonal to the rows of $A$ ($x^T v = 0$);
- In human terms, no $row(A)$ abd $N(A)$ terms are in each other
hence $\mathcal{N}(A)=\operatorname{Row}(A)^{\perp}$.
- So $\operatorname{rank}(A) + \operatorname{rank}(\mathcal(N)(A)) = N$
- Its dimension is $n-r$. If $A$ has full column rank, then $\mathcal{N}(A)={\mathbf{0}}$.
- $\textbf{Left nullspace}$ $\mathcal{N}(A^{\mathsf{T}})={\mathbf{y}\in\mathbb{R}^{m}\mid \mathbf{y}^{\mathsf{T}}A=0}$.
- This is the right nullspace of $A^{\mathsf{T}}$ and is orthogonal to $\operatorname{Col}(A)$.
- Its dimension is $m-r$.
Projection Matrix
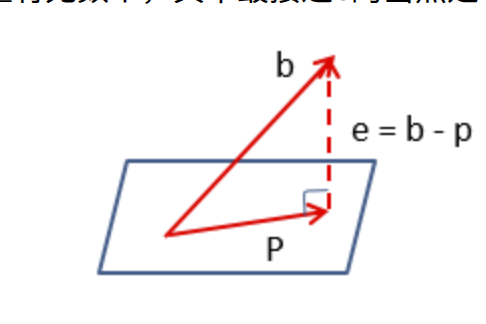
When the system \(A\mathbf{x} = \mathbf{b}\) has no exact solution (because $\mathbf{b} \notin Col(A)$), we look for the closest vector (which is mx1) \(\mathbf{p} = A\hat{\mathbf{x}}\)
lying in the column space of $A$. In other words, $\hat{\mathbf{x}}$ is chosen so that \(\|\,\mathbf{b} - A\hat{\mathbf{x}}\,\|\) is minimized; equivalently, $\mathbf{b}-\mathbf{p}$ is orthogonal to $Col(A)$.
- If $rank(A)=2$ but $n=3$, then $Col(A)$ is a plane in $\mathbb{R}^3$.
- Therefore, $p$ is a projection of b on this plane
Derivation of the Projection Matrix
- Let ${\mathbf{a}_1,\mathbf{a}_2,\dots,\mathbf{a}_r}$ be a basis for $Col(A)$. $p = A\hat{\mathbf{x}}$ Orthogonality means \(\mathbf{a}_i^T\bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr) = 0 \quad\text{for }i=1,\dots,r.\)
- Stacking these conditions gives \(A^T\bigl(\mathbf{b} - A\hat{\mathbf{x}}\bigr)=\mathbf{0}.\)
- Rearranging yields the normal equations}: \(A^T A\,\hat{\mathbf{x}} = A^T \mathbf{b}.\)
- If $A$ has full column rank $rank(A)=n$, then $A^TA$ is positive definite and invertible, one can prove this by proving “A^TA” and $A$ have the same solutions.
- $A^TA$ and $A$ have the same column rank
- So
\(\hat{\mathbf{x}} = (A^T A)^{-1} A^T \mathbf{b}.
\\
\mathbf{p} = A \hat{\mathbf{x}} = A(A^T A)^{-1} A^Tb\)
- We define projection matrix as $A(A^T A)^{-1} A^T$. It projects b onto the column space of A.
- Otherwise $A^TA$ is only positive semi-definite (singular), and one typically uses the Moore–Penrose pseudoinverse: \(\hat{\mathbf{x}} = A^+ \mathbf{b}.\)
Full Rank Factorization
Statement:
If an arbitrary matrix $A\in\R^{m\times n}$ has rank $r$, then there exist matrices $C\in\R^{m\times r}$ and $F\in\R^{r\times n}$, both of rank $r$, such that \(A = C\,F.\)
Proof:
Since $rank(A)=r$, select $r$ linearly independent columns of $A$, with indices $j_1,\dots,j_r$. We choose a basis of $Col(A)$ and put them in $C$:
\[C = \bigl[A_{\,:\,,j_1}\;\;A_{\,:\,,j_2}\;\cdots\;A_{\,:\,,j_r}\bigr] \in\R^{m\times r},\]so $rank(C)=r$. Each column $A_{\,:\,,k}$ of $A$ lies in the column space of $C$, hence there is a vector $f_k\in\R^r$ with \(A = C_1 F_1^T + C_2 F_2^T ...\) Stacking these coefficient vectors yields \(F = \bigl[F_1^T;\;F_2^T;\cdots\;F_n\bigr] \in\R^{r\times n},\) and by construction $C\,F=A$.
Finally, $rank(F)=r$ because the product of two matrices cannot have a rank larger than either matrix. This means $rank(CF)=rank(A)=r$, and $rank(F)\ge rank(CF)$. And F has r columns, $rank(F) = r$ So F’s columns are unique.
Projection When $A$ Is Not Full Column Rank Using Pseudo Inverse
When $ A \in \mathbb{R}^{m \times n} $ does not have full column rank, the matrix $ A^\top A $ is not invertible. This makes the normal equation solution \(\hat{\mathbf{x}} = (A^\top A)^{-1} A^\top \mathbf{b}\) invalid.
However, we still want to find $ \hat{\mathbf{x}} $ such that \(A\hat{\mathbf{x}} = \mathbf{p}\) where $ \mathbf{p} $ is the orthogonal projection of $ \mathbf{b} $ onto $ \operatorname{Col}(A) $.
Using Full Rank Factorization
Let $ A = F G $ be the full-rank factorization, where:
- $ F \in \mathbb{R}^{m \times r} $ has full column rank and spans $ \operatorname{Col}(A) $,
- $ G \in \mathbb{R}^{r \times n} $ has full row rank and spans $ \operatorname{Row}(A) $.
To project $ \mathbf{b} $ onto $ \operatorname{Col}(A) $, use: \(\mathbf{p} = F(F^\top F)^{-1} F^\top \mathbf{b}.\)
Solving for $\hat{\mathbf{x}}$
We solve: \(A\hat{\mathbf{x}} = F G \hat{\mathbf{x}} = \mathbf{p}.\) Left-multiplying both sides by $ (F^\top F)^{-1} F^\top $ gives: \(G \hat{\mathbf{x}} = (F^\top F)^{-1} F^\top \mathbf{b}.\)
Since $ A $ does not have full column rank, the solution set for $ \hat{\mathbf{x}} $ is infinite. Let: \(\hat{\mathbf{x}} = \mathbf{x}_t + \mathbf{x}_0,\quad \text{where } A\mathbf{x}_0 = 0.\) Then: \(A(\mathbf{x}_t + \mathbf{x}_0) = A\mathbf{x}_t.\)
We project $ \hat{\mathbf{x}} $ onto $ \operatorname{Row}(A) $ to get the unique component: \(\mathbf{x}_t = G^\top (G G^\top)^{-1} G \hat{\mathbf{x}}.\)
Substitute in $ G\hat{\mathbf{x}} $: \(\mathbf{x}_t = G^\top (G G^\top)^{-1} (F^\top F)^{-1} F^\top \mathbf{b}.\)
Final Pseudoinverse
Thus, the matrix \(A^\dagger = G^\top (G G^\top)^{-1} (F^\top F)^{-1} F^\top\) acts as a pseudoinverse of $ A $, producing the unique solution in the row space such that $ A \mathbf{x}_t $ projects $ \mathbf{b} $ onto $ \operatorname{Col}(A) $.
Pseudo Inverse Using SVD
Let $ A \in \mathbb{R}^{m \times n} $ be a matrix of rank $ r $. Its singular value decomposition (SVD) is \(A = U \Sigma V^\top\)
where:
- $ U \in \mathbb{R}^{m \times m} $ is orthogonal: $ U^\top U = I $,
- $ V \in \mathbb{R}^{n \times n} $ is orthogonal: $ V^\top V = I $,
- $ \Sigma \in \mathbb{R}^{m \times n} $ is diagonal (or block-diagonal) with singular values $ \sigma_1, \dots, \sigma_r > 0 $.
Explicitly, \(\Sigma = \begin{bmatrix} \operatorname{diag}(\sigma_1, \dots, \sigma_r) & 0 \\ 0 & 0 \end{bmatrix}.\)
The Moore–Penrose pseudoinverse is given by: \(A^\dagger = V \Sigma^\dagger U^\top\) where \(\Sigma^\dagger = \begin{bmatrix} \operatorname{diag}\left(\frac{1}{\sigma_1}, \dots, \frac{1}{\sigma_r}\right) & 0 \\ 0 & 0 \end{bmatrix}.\)
Since $ U $ and $ V $ are orthogonal, we have: \(U^\top = U^{-1}, \quad V^\top = V^{-1}.\)
The pseudoinverse $ A^\dagger $ satisfies:
- $ A A^\dagger A = A $
- $ A^\dagger A A^\dagger = A^\dagger $
- $ (A A^\dagger)^\top = A A^\dagger $
- $ (A^\dagger A)^\top = A^\dagger A $